1. Кочаны капусты
Когда вторая покупательница взяла половину оставшихся кочанов и еще полкочана, у фермера остался только один кочан. Значит, полтора кочана составляют половину того количества, которое осталось после первой продажи. Ясно, что полностью это количество равно трем. Если к этому числу прибавить полкочана, то получится половина всех кочанов, которые были у фермера. Нетрудно решить, что он принес на базар семь кочанов капусты.
2. Сколько страниц?
Из первых девяти страниц каждая нумеруется одной цифрой. Нумерация следующих 90 страниц требует 180 цифр, по две цифры на каждую страницу. Чтобы пронумеровать дальше 900 страниц, надо 2700 цифр. Значит, если бы книга содержала 999 страниц, то для ее нумерации потребовалось бы 2889 цифр (9 + 180 + 2700). На самом деле употребили 2775 цифр. Отсюда можно сделать вывод, что в книге больше 100 страниц, но меньше 999. Вычтя из 2775 то количество цифр, которое потребовалось для нумерации первых 99 страниц, то-есть 189, получим 2586. Такое число цифр оказалось необходимым, чтобы пронумеровать страницы книги начиная от 100. Разделив 2586 па 3, узнаем, что таких страниц было 862. Значит, книга содержит (862 + 99) 961 страницу.
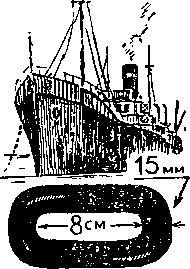
Якорная цепь
В любой цепи всякое звено соединяется с двумя соседними. Исключение составляют два крайних звена: каждое из них сцеплено только с одним звеном.
Значит, умножив длину просвета в звене на число звеньев и прибавив к произведению удвоенную толщину стержня, из которого сделана цепь, мы определим ее длину:
8 см X 685 = 5480 см; 5480 см + 3 см = 5483 см = 54 м 83 см.
Лишняя деталь.
Первый вариант. Надо взять любые шесть деталей и положить их по три на чашки весов. Это первое взвешивание может дать различите результаты:
1) весы будут находиться в равновесии;
2) одна чашка весов опустится.
В первом случае ясно, что более легкой является одна из двух деталей, не лежащих на весах. Если положить эти детали по одной на чашки весов, то, конечно, приподнимется та чашка, на которую попадет более легкая деталь.
Во втором случае очевидно, что более легкая — одна из трех деталей, находящихся на той чашке весов, которая приподнялась.
Освободив весы, надо взять из этих трех деталей любые две и положить их по одной на чашки весов. Если весы уравновесятся, это будет означать, что не положена на весы более легкая деталь.
Если же одна из чашек весов приподнимется, то, значит, на ней лежит более легкая деталь.
Второй вариант. В целях более сжатого изложения обозначим через х деталь, которую надо выделить.
При каждом взвешивании будем называть первым случаем такое положение, когда чашки весов приходят в равновесие. Вторым случаем назовем положение, при котором равновесия нет.
Первое взвешивание. Берем наугад любые четыре детали и кладем их попарно на чашки весов.
Вывод в первом случае: детали х нет в той четверке, которая лежит па весах.
Вывод во втором случае: деталь х — одна из двух деталей, которые находятся на правой или на левой чашке весов.
Дальше мы можем пользоваться только теми четырьмя деталями, среди которых находится деталь х.
Второе взвешивание. Откладываем в сторону любые две детали, а другие две кладем по одной на чашки весов.
Вывод в первом случае: деталь х опять не попала на весы.
Вывод во втором случае: деталь х находится на правой или на левой чашке весов.
Третье взвешивание. Освобождаем какую-либо чашку весов и помещаем на нее одну из деталей, которые мы отложили в сторону перед вторым взвешиванием.
Вывод в первом случае: деталь х — это та деталь из двух отложенных, которая при третьем взвешивании не попала на весы.
Вывод во втором случае: деталь х только что положена нами на весы.